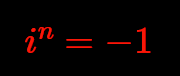
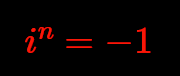
The main surprise for me was the fact, that this vector multiplication works at the same time according to their dimension in the vector space and in all its atoms and molecules. It is just the matter on which basis we transform our view.

To bring all the analogies to a point, I would like to define two last words: reference space and origination.

Reference spaces are all vector spaces $\mathbb R^n$ and all their molecules and atoms and zero.
Because zero is a 0-dimensional space, it is more a reference point than a space. It is the origin of all reference spaces and the only intersection of all of them. But some of the analogies makes no sense without a genuine dimensional expansion...

Origionation of a vector is the smallest it containing reference space. This is the linear combination of all atoms, in which the vector is not zero.

The perpendicular vector subspace in zero is for every reference space another reference space. Every vector is zero in the perpendicular reference space of its origination.

For n=1 and n=2 the vector spaces are atomic reference spaces. Their perpendicular reference spaces are the reference point, and no further zero divisors exsist.

For $n \gt 2$ the reference point is unfolding into multiple atoms. And every of their linear combination is another reference space.

Zero divisor originate always from $(d \lt n)$-dimensional reference spaces (they are at least in one atom zero),
only non zero divisors originate from the vector space, and they do this always (they are non zero in every atom).

In every reference space there is one element, which is multiplicative neutral to all elements of the reference space, its real unit, which is always the perpendicular projection of the real unit of the vector space into the reference space.

The units of reference spaces have always the length $\sqrt{d \over n}$.

Only the real unit of the reference spaces have a non zero real coordinate, which is always ${d \over n}$, all non real units in all reference spaces start with 0 as real coordinate.

The real unit of a refence space is always the sum of the real units of the it combining atoms.

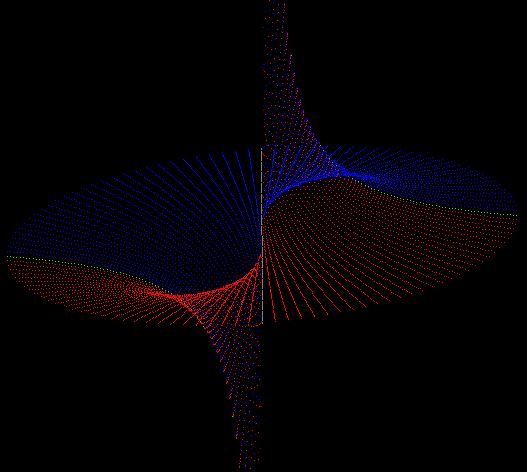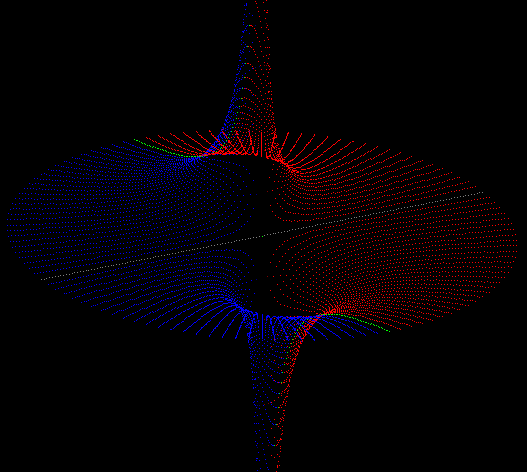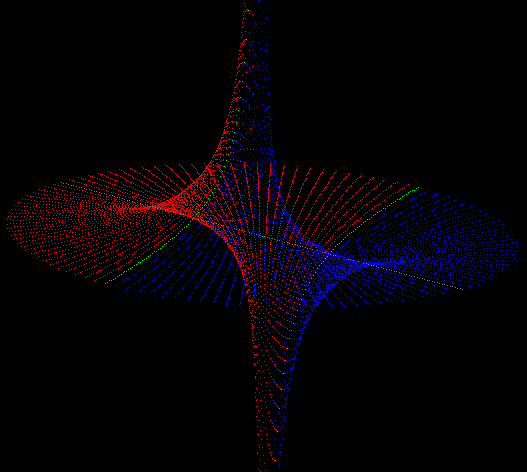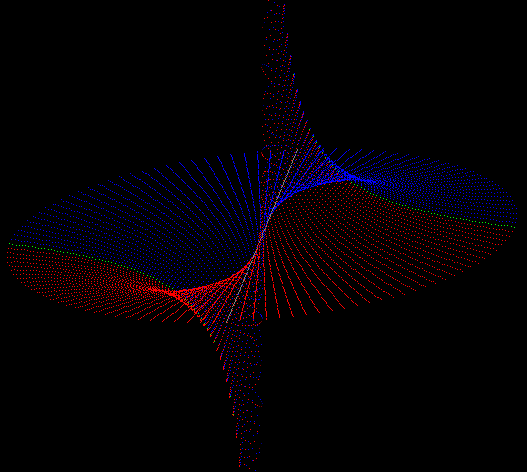
This vector multiplication is from the geometrical view a projective strech-rotation:
Every factor of the product projects into its origination, because it is zero in the perpendicular reference space of its origin. This is the projective part, which is not reversible.
The strech-rotation take part in every atom of the intersection of the origination of all factors. This is reversible as we know from the multiplication in the complex plane.

Even most reference spaces contain only zero divisors, so no element has a generally multiplicative inverse element for every vector of the vector space. Within the origination has every vector except zero a multiplicative revertive element. The product of 'revertive elements' is always the real unit of their common origination.

All known operations and functions from real - and complex analysis are applicable to $\mathbb R^n$-vectors, as long they are executable in all atoms.

The atoms speak clear: complex is better than real. Complex atoms are regular, one real atom appear only, if there isn't enough space, as a leftover or remainder.

And because complex is very important, the next page might also be of interest...