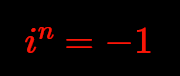
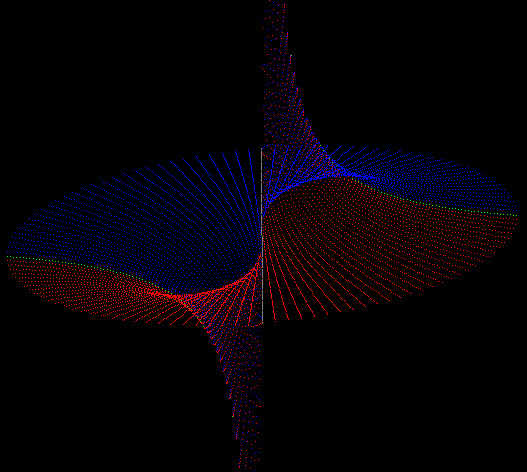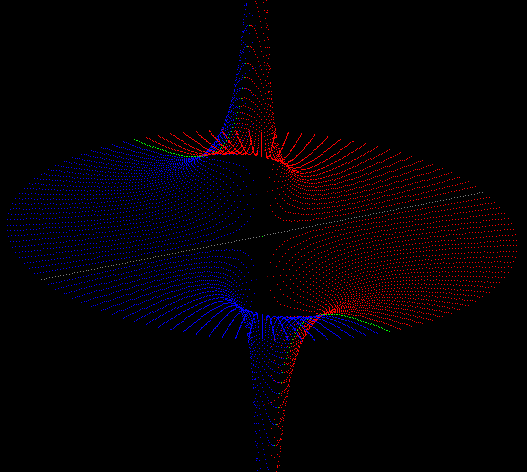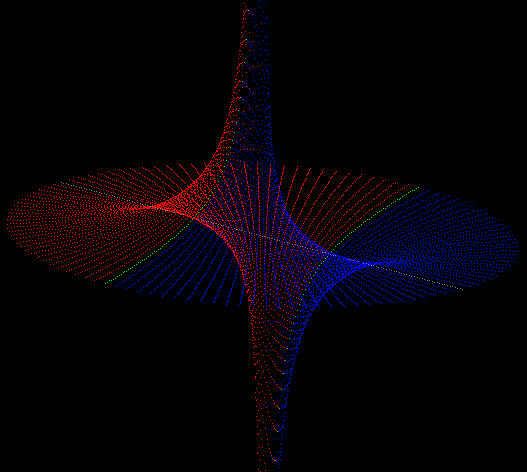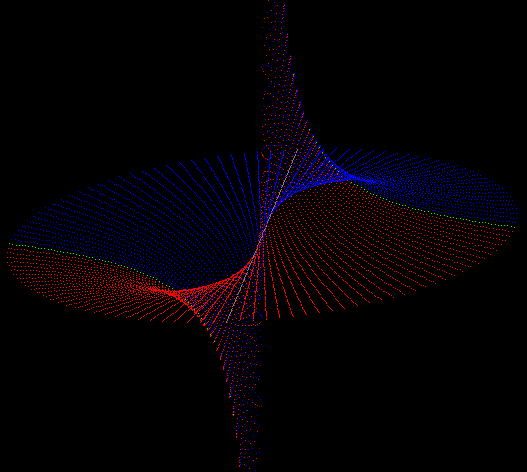
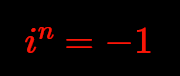
The atomic transformation has some really astonishing conclusions:
Based on the facts, that the vector multiplication works effectively the same time in all atoms and in the vector space according to their dimensions, and that the vector space the linear combination of all its atoms is, we can say, that every linear combination of atoms with the dimension d together must be isomorphic to d-dimensional vector space.

Molecules of a vectorspace are all linear combinations of not all atoms of the vector space.

The $(d \times n)$-matrix of a molecule with all its units as columns should contain the indices of all involved atoms in its index and it can be calculated by taking out from $A_n$ the columns of all not involved atoms and multiplying it with the inverse of the d-dimensional Atomic basis:$M_{kl...}=\left(\hat r_k, \hat i_k, \hat r_l, \hat r_l, \ldots \right) \cdot A_d^{-1}$.

For a full molecular basis we have to place back the units of all not involved atoms, or some other molecular combinations of them.

The molecular transformation of $\vec x$ and its multipplication matrix will show d-dimensional part matrices along the diagonal according to the involved moelcules and atoms. Here a complicated example from n=11:

$M''_{ {\color{green}013}+{\color{red}25}+{\color{yellow}4} } = \begin{pmatrix} {\color{green}x''_0} & {\color{green}-x''_7} & {\color{green}-x''_6} & {\color{green}-x''_3} & 0 & 0 & {\color{green}-x''_2} & {\color{green}-x''_1} & 0 & 0 & 0 \\ {\color{green}x''_1} & {\color{green}x''_0} & {\color{green}-x''_7} & {\color{green}-x''_6} & 0 & 0 & {\color{green}-x''_3} & {\color{green}-x''_2} & 0 & 0 & 0 \\ {\color{green}x''_2} & {\color{green}x''_1} & {\color{green}x''_0} & {\color{green}-x''_7} & 0 & 0 & {\color{green}-x''_6} & {\color{green}-x''_3} & 0 & 0 & 0 \\ {\color{green}x''_3} & {\color{green}x''_2} & {\color{green}x''_1} & {\color{green}x''_0} & 0 & 0 & {\color{green}-x''_7} & {\color{green}-x''_6} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\color{red}x''_4} & {\color{red}-x''_{10}} & 0 & 0 & 0 & 0 & {\color{red}-x''_5} \\ 0 & 0 & 0 & 0 & {\color{red}x''_5} & {\color{red}x''_4} & 0 & 0 & 0 & 0 & {\color{red}-x''_{10}} \\ {\color{green}x''_6} & {\color{green}x''_3} & {\color{green}x''_2} & {\color{green}x''_1} & 0 & 0 & {\color{green}x''_0} & {\color{green}-x''_7} & 0 & 0 & 0 \\ {\color{green}x''_7} & {\color{green}x''_6} & {\color{green}x''_3} & {\color{green}x''_2} & 0 & 0 & {\color{green}x''_1} & {\color{green}x''_0} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\color{yellow}x''_8} & {\color{yellow}-x''_9} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\color{yellow}x''_9} & {\color{yellow}x''_8} & 0 \\ 0 & 0 & 0 & 0 & {\color{red}x''_{10}} & {\color{red}x''_5} & 0 & 0 & 0 & 0 & {\color{red}x''_4} \\ \end{pmatrix}$.

That was a lot of talk, without any evidence or proof yet...