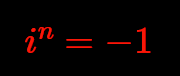
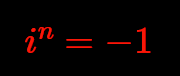
If you are really interested in any of the following proofs, click on it at your own risk!
If it is too ugly, you can close it with a second click!

1. Commutativity

   Index transformation $j \rightarrow k-j$ in the first sum, and $j \rightarrow n+k-j$ in the second sum:

   $(\vec x \cdot \vec y)_k = \sum\limits_{j=0}^{k} x_{k-j} y_j - \sum\limits_{j=k+1}^{n-1} x_{n+k-j} y_j = \sum\limits_{j=0}^{k} x_j y_{k-j} - \sum\limits_{j=k+1}^{n-1} x_j y_{n+k-j} = \sum\limits_{j=0}^{k} y_{k-j} x_j - \sum\limits_{j=k+1}^{n-1} y_{n+k-j} x_j = (\vec y \cdot \vec x)_k$

2. Associativity

   $((\vec x \cdot \vec y) \cdot \vec z)_k=\sum\limits_{j=0}^{k} (\vec x \cdot \vec y)_{k-j}z_j - \sum\limits_{j=k+1}^{n-1} (\vec x \cdot \vec y)_{n+k-j}z_j=$
   $=\sum\limits_{j=0}^{k} {\left( \sum\limits_ {i=0}^{k-j}{x_{k-j-i}y_i}- \sum\limits_{i=k-j+1}^{n-1}{x_{n+k-j-i}y_i} \right) z_j} - \sum\limits_ {j= k+1}^{n-1} {\left( \sum\limits_ {i=0}^{n+k-j} {x_{n+k-j-i}y_i} - \sum\limits_ {i=n+k-j+1}^{n-1} {x_{2n+k-j-i}y_i}\right) z_j}=$
   $=\sum\limits_{j=0}^{k} {\sum\limits_ {i=0}^{k-j}{x_{k-j-i}y_i z_j}}- \sum\limits_{j=0}^{k} {\sum\limits_{i=k-j+1}^{n-1}{x_{n+k-j-i}y_i z_j}} - \sum\limits_ {j= k+1}^{n-1} {\sum\limits_ {i=0}^{n+k-j} {x_{n+k-j-i}y_i z_j}} + \sum\limits_ {j= k+1}^{n-1} {\sum\limits_ {i=n+k-j+1}^{n-1} {x_{2n+k-j-i}y_i z_j}}=$
   $={\sum\limits_{i,j}^{} x_i y_ j z_{k-i-j} - \sum\limits_{i,j}^{} x_i y_ j z_{n+k-i-j} + \sum\limits_{i,j}^{} x_i y_ j z_{2 n+k-i-j} }=$
   $=\sum\limits_{j=0}^{k} {\sum\limits_ {i=0}^{k-j}{z_{k-j-i}y_i x_j}}- \sum\limits_{j=0}^{k} {\sum\limits_{i=k-j+1}^{n-1}{z_{n+k-j-i}y_i x_j}}- \sum\limits_ {j= k+1}^{n-1} {\sum\limits_ {i=0}^{n+k-j} {z_{n+k-j-i}y_i x_j}}+ \sum\limits_ {j= k+1}^{n-1} {\sum\limits_ {i=n+k-j+1}^{n-1} {z_{2n+k-j-i}y_i x_j}}=$
   $=\sum\limits_{j=0}^{k} {\left( \sum\limits_ {i=0}^{k-j}{z_{k-j-i}y_i}- \sum\limits_{i=k-j+1}^{n-1}{z_{n+k-j-i}y_i} \right) x_j} - \sum\limits_ {j= k+1}^{n-1} {\left( \sum\limits_ {i=0}^{n+k-j} {z_{n+k-j-i}y_i} - \sum\limits_ {i=n+k-j+1}^{n-1} {z_{2n+k-j-i}y_i}\right) x_j}=$
   $=\sum\limits_{j=0}^{k} (\vec z \cdot \vec y)_{k-j}x_j - \sum\limits_{j=k+1}^{n-1} (\vec z \cdot \vec y)_{n+k-j}x_j=((\vec z \cdot \vec y) \cdot \vec x)_k \overset{(1.)}{=} (\vec x \cdot (\vec y \cdot \vec z))_k$

3. Distributivity

   $(\vec x \cdot (\vec y + \vec z))_k=\sum\limits_{j=0}^{k} x_{k-j}(y_j+z_j) - \sum\limits_{j=k+1}^{n-1} x_{n+k-j}(y_j+z_j)=\sum\limits_{j=0}^{k} x_{k-j}y_j+x_{k-j}z_j - \sum\limits_{j=k+1}^{n-1} x_{n+k-j}y_j+x_{n+k-j}z_j=$
   $=\sum\limits_{j=0}^{k} x_{k-j}y_j + \sum\limits_{j=0}^{k} x_{k-j}z_j- \sum\limits_{j=k+1}^{n-1} x_{n+k-j}y_j - \sum\limits_{j=k+1}^{n-1} x_{n+k-j}z_j=$
   $=\sum\limits_{j=0}^{k} x_{k-j}y_j - \sum\limits_{j=k+1}^{n-1} x_{n+k-j}y_j + \sum\limits_{j=0}^{k} x_{k-j}z_j - \sum\limits_{j=k+1}^{n-1} x_{n+k-j}z_j=(\vec x \cdot \vec y + \vec x \cdot \vec z)_k$

4. Multiplicative identity

   Because the multiplication matrix of $\hat e_0$ is the identity matrix $M_{\hat e_0} = I_n$,
   $\hat e_0$ must be obviously the neutral element of multiplication.

5. Power row of the imaginary unit of the vector space

   The multiplication matrix of i: $M_i=\begin{pmatrix} 0 & 0 & 0 & \cdots & 0 & -1 \\ 1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 1 & 0 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \ddots & 0 & 0 \\ 0 & 0 & 0 & \cdots & 1 & 0 \\ \end{pmatrix}$ shows clearly, that i as factor shift down all coodinates of another factor and the last coordinate, which would 'fall out' coming back with altered sign in the first coordinate.

   This means with exception of the last unit vector just the next one: $\forall j \lt (n-1): \space\space i \cdot \hat e_j = \hat e_{j+1}$, and for the last unit vector: $i \cdot \hat e_{n-1} = \hat e_0 = -1$.

   The 0-th power of every vector must be the neutral element of multiplication, also for i: $i^0=\hat e_0$.

   All together: $\hat e_j = i^j = -i^{j+n}$. The power row of the imaginary unit runs cyclically through all units and their additive inverses.

6. Proofs on the circle (needed for further proofs)
   1. If k is not a multiple of n ($\forall k \ne n \cdot l$):
      $\sum\limits_ {j=0}^{n-1} {\sin \left(x+ {{kj} \over n} 2 π \right)}$$=\sum\limits_ {j=0}^{n-1} {\cos \left(x+ {{kj} \over n} 2 π \right)} \overset{!}{=}0$

      The argument of the trigonometric functions $\left(x+ {{kj} \over n} 2 π\right)$ segregates the circle from the starting radian x in more than one equal pieces. The vecors to these points can be rearranged to a regular polygon. This means the sum of these vectors must be zero in both coordinates. The sinus and cosinus from the formula are the perpendicular projections of these points onto the axis, so their sums also must be zero.

   2. If k is a multiple of n ($\forall k = n \cdot l$):
      $\sum\limits_ {j=0}^{n-1} {\sin \left(x+ {{kj} \over n} 2 π \right)} \overset{!}{=}n \sin(x)$

      $\sum\limits_ {j=0}^{n-1} {\sin \left(x+ {{kj} \over n} 2 π \right)} = \sum\limits_{j=0}^{n-1}\sin(x+lj2π) =n \sin(x)$

   3. Same for the cosinus ($\forall k = n \cdot l$):
      $\sum\limits_ {j=0}^{n-1} {\cos \left(x+ {{kj} \over n} 2 π \right)} \overset{!}{=}n \cos(x)$

      $\sum\limits_ {j=0}^{n-1} {\cos \left(x+ {{kj} \over n} 2 π \right)} = \sum\limits_{j=0}^{n-1}\cos(x+lj2π) =n \cos(x)$

7. Length of the atomic units
   1. $\left| {\hat r_k} \right| \overset{!}{=} \sqrt {d_k \over n}$:

      $\left| {\hat r_k}\right|=$$\sqrt {\sum\limits_{j=0}^{n-1}{\left( {d_k \over n} \cos \left({{(2k+1)j}\over n} π \right) \right)^2}}=$ $\sqrt{{d_k^2 \over {2 n^2}} \sum\limits_ {j=0}^{n-1}{\cos(0)+\cos \left({{(2 k+1)j}\over n} π \right)}}=$
      $=\begin{cases} \overset {(6.a)}{=} \sqrt{{d_k^2 \over {2 n^2}} \sum\limits_ {j=0}^{n-1}{\cos(0)}} = \sqrt {d_k \over n} & \forall n \gt 2 k+1 \Leftrightarrow d_k=2 \\ \color{blue}{\overset {(6.c)}{=} \sqrt{{d_k^2 \over {2 n^2}} \sum\limits_ {j=0}^{n-1}{\cos(0)+\cos (0)}} = \sqrt{d_k^2 \over n} = \sqrt {d_k \over n}} & \color{blue}{\forall n = 2 k+1 \Leftrightarrow d_k=1} \end{cases}$
      

   2. $\left| {\hat i_k} \right| \overset{!}{=} \sqrt {2 \over n}$:

      $\left|\hat i_k\right|=$$\sqrt {\sum\limits_{j=0}^{n-1}{\left({2 \over n} \sin \left({{(2 k+1)j}\over n} π \right) \right)^2}}=$ $\sqrt{{2 \over {n^2}} \sum\limits_ {j=0}^{n-1}{\cos(0)-\cos \left({{(2 k+1)j}\over n} π \right)}} \overset{(6.a)}{=} \sqrt{{2 \over {n^2}} \sum\limits_ {j=0}^{n-1}{\cos(0)}}=$ $\sqrt{2 \over {n} }$

8. Orthogonality of the atomic basis
   1. $\hat r_k \circ \hat r_l \overset{!}{=} 0 {\color{black}{aaaa}} \forall (k \ne l)$:

      $\hat r_k \circ \hat r_l=$${{d_k d_l} \over { n^2}} \sum\limits_{j=0}^{n-1} {\cos \left( {{(2k+1)j} \over { n}} π \right) \cdot \cos \left( {(2l+1)j} \over { n} π \right)}=$ ${{d_k d_l} \over { 2 n^2}} \sum\limits_{j=0}^{n-1} { \left(\cos \left({{2 (k-l) j}\over { n}} π \right)+\cos \left( {{2 (k+l+1) j} \over { n}} π \right) \right)} \overset {(6.a)}{=} 0+0$.

   2. $\hat i_k \circ \hat r_l \overset{!}{=} 0 {\color{black}{aaaa}} \forall k,l$:

      $\hat i_k \circ \hat r_l=$${{2 d_l} \over { n^2}}\sum\limits_{j=0}^{n-1} {\sin \left( {{(2 k+1)j} \over { n}} π \right) \cdot \cos \left( {{(2 l+1)j} \over { n}} π \right)}=$ ${{d_l} \over { n^2}} \sum\limits_{j=0}^{n-1} { \left(\sin \left({{2 (l-k) j}\over { n}} π \right)+\sin \left( {{2 (l+k+1) j} \over { n}} π \right) \right)} \overset {(6.a)}{=} 0+0$.

   3. $\hat i_k \circ \hat i_l \overset{!}{=} 0 {\color{black}{aaaa}} \forall (k \ne l)$:

      $\hat i_k \circ \hat i_l=$${{ 4} \over { n^2}} \sum\limits_{j=0}^{n-1} {\sin \left({{(2 k+1)j} \over { n}} π \right) \cdot \sin \left({{(2 l+1)j} \over { n}} π \right)}=$ ${{ 2} \over { n^2}} \sum\limits_{j=0}^{n-1} { \left(\cos \left({{2 (k-l) j}\over { n}} π \right)-\cos \left( {{2 (k+l+1) j} \over { n}} π \right) \right)} \overset {(6.a)}{=} 0-0$.

9. Real unit square

   ${\hat r_k}^2 \overset{!}{=} \hat r_k$ (proof in every single coordinate):

   $({\hat r}_{k} ^2)_l$$=\sum\limits_{j=0}^{l}{r_{k_{l-j}} r_{k_{j}}} - \sum\limits_{j=l+1}^{n-1}{r_{k_{n+l-j}} r_{k_{j}}}=$
   $=\sum\limits_{j=0}^{l}{{{ d_k \over n}} \cos \left({{(2 k+1)(l-j)} \over { n}} π \right) {{ d_k \over n}} \cos \left({{(2 k+1)j} \over { n}} π \right)} - \sum\limits_{j=l+1}^{n-1}{{{ d_k \over n}} \cos \left({{(2 k+1)(n+l-j)} \over { n}} π \right) {{ d_k \over n}} \cos \left({{(2 k+1)j} \over { n}} π \right)}=$
   $={{ d_k^2 \over {n^2}}} \sum\limits_{j=0}^{l}{\cos \left({{(2 k+1)(l-j)} \over { n}} π \right) \cos \left({{(2 k+1)j} \over { n}} π \right)} + {{ d_k^2 \over {n^2}}} \sum\limits_{j=l+1}^{n-1}{\cos \left({{(2 k+1)(l-j)} \over { n}} π \right) \cos \left({{(2 k+1)j} \over { n}} π \right)}=$
   $={{ d_k^2 \over {n^2}}} \sum\limits_{j=0}^{n-1}{\cos \left({{(2 k+1)(l-j)} \over { n}} π \right) \cos \left({{(2 k+1)j} \over { n}} π \right)}$ $={{ d_k^2 \over {2 n^2}}} \sum\limits_{j=0}^{n-1}{\cos \left({{(2 k+1)(l-2 j)} \over { n}} π \right) + \cos \left({{(2 k+1)l} \over { n}} π \right)}=$

   1. $\forall n \gt 2 k+1 \Leftrightarrow d_k=2$:

      $\overset {(6.)}{=}{d^2\over{2 n^2}}\sum\limits_{j=0}^{n-1}{\cos\left({{(2k+1)l}\over{n}}π\right)}$$={d^2 \over {2n}} \cos \left( {{(2k+1)l}\over{n}}π \right)={d \over n}\cos \left({{(2k+1)l}\over{n}}π \right)$ $=(\hat r_k)_l$.

   2. $\forall n = 2 k+1 \Leftrightarrow d_k=1$:

      $={d^2 \over {2n^2}} \sum\limits_{j=0}^{n-1}{\cos \left({{(2k+1)l-2(2k+1)j} \over {n}} π \right) + \cos \left({{(2 k+1)l} \over {n}} π \right)}$$\overset {(6.)}{=} {d^2 \over {2 n^2}} \sum\limits_{j=0}^{n-1}{2 \cos \left({{(2 k+1)l} \over { n}} π \right)={d \over n} \cos \left({{(2 k+1)l} \over {n}} π \right) = ({\hat r}_k)_l}$

10. Imaginary unit square

    ${\hat i_k}^2 \overset{!}{=} - \hat r_k$ (proof in every single coordinate):

    $({\hat i_k}^2)_l$$=\sum\limits_{j=0}^{l}{i_{k_{l-j}} i_{k_{j}}} - \sum\limits_{j=l+1}^{n-1}{i_{k_{n+l-j}} i_{k_{j}}}$
    $=\sum\limits_{j=0}^{l}{{{ 2 \over n}} \sin \left({{(2 k+1)(l-j)} \over { n}} π \right) {{ 2 \over n}} \sin \left({{(2 k+1)j} \over { n}} π \right)} - \sum\limits_{j=l+1}^{n-1}{{{ 2 \over n}} \sin \left({{(2 k+1)(n+l-j)} \over { n}} π \right) {{ 2 \over n}} \sin \left({{(2 k+1)j} \over { n}} π \right)}=$
    $={4 \over n^2} \sum\limits_{j=0}^{l}{\sin \left({{(2 k+1)(l-j)} \over { n}} π \right) \sin \left({{(2 k+1)j} \over { n}} π \right)} + {{ 4 \over n^2}} \sum\limits_{j=l+1}^{n-1}{\sin \left({{(2 k+1)(l-j)} \over { n}} π \right) \sin \left({{(2 k+1)j} \over { n}} π \right)}=$
    $={4 \over n^2} \sum\limits_{j=0}^{n-1}{\sin \left({{(2 k+1)(l-j)} \over { n}} π \right) \sin \left({{(2 k+1)j} \over { n}} π \right)}$ $={2 \over n^2} \sum\limits_{j=0}^{n-1}{\cos \left({{(2 k+1)(l-2 j)} \over { n}} π \right) - \cos \left({{(2 k+1)l} \over {n}} π \right)} \overset {(6.a)}{=}$
    $\overset {(6.a)}{=}{2 \over {n^2}} \sum\limits_{j=0}^{n-1}{-\cos \left({{(2 k+1)l} \over {n}} π \right)}$ $=- {2 \over n}\cos \left({{(2 k+1)l} \over { n}} π \right)$ $=(-{\hat r}_k)_l$

11. Product of real and imaginary unit of the same atom

    $\hat i_k \cdot \hat r_k \overset{!}{=} \hat i_k$:

    $(\hat i_k \cdot {\hat r}_k)_l$$=\sum\limits_{j=0}^{l}{i_{k_{l-j}} r_{k_{j}}} - \sum\limits_{j=l+1}^{n-1}{i_{k_{n+l-j}} r_{k_{j}}}=$
    $=\sum\limits_{j=0}^{l}{{2 \over n} \sin \left({{(2k+1)(l-j)} \over {n}} π \right) {2 \over n} \cos \left({{(2k+1)j} \over {n}} π \right)} - \sum\limits_{j=l+1}^{n-1}{{{ 2 \over n}} \sin \left({{(2 k+1)(n+l-j)} \over {n}} π \right) {2 \over n} \cos \left({{(2 k+1)j} \over {n}} π \right)}=$
    $={4 \over n^2} \sum\limits_{j=0}^{l}{\sin \left({{(2k+1)(l-j)} \over {n}} π \right) \cos \left({{(2k+1)j} \over {n}} π \right)} + {4 \over n^2} \sum\limits_{j=l+1}^{n-1}{\sin \left({{(2 k+1)(l-j)} \over {n}} π \right) \cos \left({{(2 k+1)j} \over {n}} π \right)}=$
    $={4 \over n^2} \sum\limits_{j=0}^{n-1}{\sin \left({{(2k+1)(l-j)} \over {n}} π \right) \cos \left({{(2k+1)j} \over {n}} π \right)}$ $={2 \over n^2} \sum\limits_{j=0}^{l}{\sin \left({{(2k+1)(l-2j)} \over {n}} π \right) + \sin \left({{(2k+1)l} \over {n}} π \right)} \overset {(6.a)}{=}$ ${2 \over n^2} \sum\limits_{j=0}^{l}{\sin \left({{(2k+1)l} \over {n}} π \right)}=$
    $={2 \over n} \sin \left({{(2k+1)l}\over{n}} π \right)$ $=(\hat i_k)_l$

12. Product of units from different atoms
    1. $\hat r_k \cdot \hat r_l \overset{!}{=} 0 {\color{black}{aaaa}}\forall k \ne l$:

       $({\hat r}_k \cdot {\hat r}_l)_m$$=\sum\limits_{j=0}^m{r_{k_{m-j}} r_{l_j}} -\sum\limits_{j=m+1}^{n-1}{r_{k_{n+m-j}} r_{l_j}}=$
       $=\sum\limits_{j=0}^m{{d_k \over {n}}\cos \left({{(2 k+1)(m-j)} \over {n}} π \right) {d_l \over { n }}\cos \left({{(2 l+1)j} \over { n}} π \right) } -\sum\limits_{j=m+1}^{n-1}{{d_k \over {n}}\cos \left({{(2 k+1)(n+m-j)} \over {n}} π \right) {d_l \over {n}}\cos \left({{(2 l+1)j} \over {n}} π \right) }=$
       $={{d_k d_l} \over {n^2}}\sum\limits_{j=0}^{m}{\cos \left({{(2 k+1)(m-j)} \over {n}} π \right) \cos \left({{(2 l+1)j} \over { n}} π \right) } + {{d_k d_l}\over {n^2}}\sum\limits_{j=m+1}^{n-1}{\cos \left({{(2 k+1)(m-j)} \over {n}} π \right) \cos \left({{(2 l+1)j} \over {n}} π \right) }=$
       $={{d_k d_l} \over {n^2}} \sum\limits_{j=0}^{n-1}{\cos \left({{(2 k+1)(m-j)} \over {n}} π \right) \cos \left({{(2 l+1)j} \over { n}} π \right)}$ $={{d_k d_l} \over {2 n^2}} \sum\limits_{j=0}^{n-1}{\cos \left({{(2 k+1)m-2(k+l+1)j} \over {n}} π \right) + \cos \left({{(2 k+1)m+2(l-k)j} \over {n}} π \right)} \overset{(6.a)}{=} 0+0$

    2. $\hat i_k \cdot \hat r_l \overset{!}{=} 0 {\color{black}{aaaa}}\forall k \ne l$:

       $(\hat i_k \cdot \hat r_l)_m$$=\sum\limits_{j=0}^m{i_{k_{m-j}} r_{l_j}} -\sum\limits_{j=m+1}^{n-1}{i_{k_{n+m-j}} r_{l_j}}=$
       $=\sum\limits_{j=0}^m{{d_k \over {n}}\sin \left({{(2 k+1)(m-j)} \over {n}} π \right) {d_l \over {n}}\cos \left({{(2l+1)j} \over {n}} π \right) } -\sum\limits_{j=m+1}^{n-1}{{d_k \over {n}}\sin \left({{(2 k+1)(n+m-j)} \over {n}} π \right) {d_l \over {n}}\cos \left({{(2 l+1)j} \over {n}} π \right) }=$
       $={{d_k d_l}\over { n^2 }} \sum\limits_{j=0}^{m}{\sin \left({{(2 k+1)(m-j)} \over { n}} π \right) \cos \left({{(2l+1)j} \over {n}} π \right) } + {{d_k d_l}\over {n^2}}\sum\limits_{j=m+1}^{n-1}{\sin \left({{(2 k+1)(m-j)} \over {n}} π \right) \cos \left({{(2 l+1)j} \over {n}} π \right) }=$
       $={{d_k d_l} \over { n^2 }} \sum\limits_{j=0}^{n-1}{\sin \left({{(2 k+1)(m-j)} \over { n}} π \right) \cos \left({{(2l+1)j} \over {n}} π \right)}$ $={{d_k d_l} \over { 2 n^2 }} \sum\limits_{j=0}^{n-1}{\sin \left({{(2 k+1)m-2(k+l+1)j} \over { n}} π \right) + \sin \left({{(2k+1)m+2(l-k)j} \over {n}} π \right)} \overset {(6.a)}{=} 0+0$

    3. $\hat i_k \cdot \hat i_l \overset{!}{=} 0 {\color{black}{aaaa}}\forall k \ne l$:

       $(\hat i_k \cdot \hat i_l)_m$$=\sum\limits_{j=0}^{m}{i_{k_{m-j}} i_{l_j}} -\sum\limits_{j=m+1}^{n-1}{i_{k_{n+m-j}} i_{l_j}}=$
       $=\sum\limits_{j=0}^{m}{{d_k \over {n}}\sin \left({{(2 k+1)(m-j)} \over {n}} π \right) {d_l \over { n }}\sin \left({{(2 l+1)j} \over { n}} π \right) } -\sum\limits_{j=m+1}^{n-1}{{d_k \over { n }}\sin \left({{(2 k+1)(n+m-j)} \over {n}} π \right) {d_l \over { n }}\sin \left({{(2 l+1)j} \over { n}} π \right) }=$
       $={{d_k d_l}\over { n^2 }}\sum\limits_{j=0}^{m}{\sin \left({{(2 k+1)(m-j)} \over { n}} π \right) \sin \left({{(2 l+1)j} \over { n}} π \right) } +{{d_k d_l}\over { n^2 }}\sum\limits_{j=m+1}^{n-1}{\sin \left({{(2 k+1)(m-j)} \over { n}} π \right) \sin \left({{(2 l+1)j} \over { n}} π \right) }=$
       $={{d_k d_l} \over { n^2 }} \sum\limits_{j=0}^{n-1}{\sin \left({{(2 k+1)(m-j)} \over { n}} π \right) \sin \left({{(2 l+1)j} \over { n}} π \right)}$ $={{d_k d_l} \over { 2 n^2 }} \sum\limits_{j=0}^{n-1}{\cos \left({{(2 k+1)m-2(k+l+1)j} \over { n}} π \right) -\cos \left({{(2 k+1)m+2(l-k)j} \over {n}} π \right)} \overset{(6.a)}{=} 0-0$

13. Inverse of the atomic basis (needed for further proofs)

    $A_n^{-1} \overset {!}{=} \left( {n \over 2} \hat r_0, {n \over 2} \hat i_0, {n \over 2} \hat r_1, {n \over 2} \hat i_1, \ldots {\color{blue}{,n \hat r_k}} \right)^T$:
    With $\hat a_k$ as the k-th atomic unit in $A_n$, to show $A_n^{-1} \cdot A_n \overset {!}{=} I_n$ (in every coordinate):

    $(A_n^{-1} \cdot A_n)_{i,j} = {n \over d} \hat a_i \circ \hat a_j = \begin{cases} \forall i=j: & {n \over d} \hat a_i \circ \hat a_i = {n \over d} \cdot \left|\hat a_i\right|^2 \overset {(7.)}{=} {n \over d} \cdot {d \over n} = 1 \\ \forall i \ne j: & {n \over d} \hat a_i \circ \hat a_j \overset {(12.)}{=} 0 \end{cases}$

14. Naming convention for futher proofs (to minimize the index chaos)
    $\alpha = A_d^{-1} \in \mathbb R^{d \times d}$: the inverse of the d-dimensional atomic basis,
    $\beta = \left( \hat r_{l_0}, \hat i_{l_0}, \hat r_{l_1}, \hat i_{l_1}, \ldots \right) \in \mathbb R^{d \times n}$: the ordered collection of the involved atomic units,
    $\gamma = \beta \cdot \alpha \in \mathbb R^{d \times n}$: the matrix of the molecule.
    $\hat \beta_m$: the m-th column (atomic unit vector) of $\beta$.
    $\hat \gamma_m$: the m-th column (molecular unit vector) of $\gamma$.
15. Molecular units
    1. $d=2k$ (only complex atoms involved):

       $\gamma_{i,j}=(\beta \cdot \alpha)_{i,j}=\sum\limits_{m=0}^{d-1}{\beta_{i,m}\alpha_{m,j}}$ $=\sum\limits_{m=0}^{k-1}{\beta_{i,2 m}\alpha_{2 m, j}+\beta_{i,2 m+1}\alpha_{2 m+1,j}}=$
       $=\sum\limits_{m=0}^{k-1}{{2 \over n} \cos \left({{(2l_m +1)i} \over n} \pi \right) \cos \left({{(2 m +1)j}\over d} \pi \right) + {2 \over n} \sin \left({{(2 l_m +1)i}\over n} \pi \right) \sin \left({{(2 m +1)j}\over d} \pi \right)}=$
       $={1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{d(2l_m +1)i-n(2 m+1)j}\over {nd}} \pi \right)+ \cos \left({{d(2l_m +1)i+n(2m+1)j}\over {nd}} \pi \right)+$ $+{1 \over n} \sum\limits_{m=0}^{k-1}\cos \left({{d(2l_m +1)i-n(2m+1)j}\over {nd}} \pi \right)-\cos \left({{d(2l_m +1)i+n(2m+1)j}\over {nd}} \pi \right)=$
       $={2 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{d(2l_m +1)i-n(2m+1)j}\over {nd}} \pi \right)$

    2. $d=2k \color{blue}+1$ (real atom involved):

       $\gamma_{i,j}=(\beta \cdot \alpha)_{i,j}=\sum\limits_{m=0}^{d-1}{\beta_{i,m}\alpha_{m,j}}$ $=\left(\sum\limits_{m=0}^{k-1}{\beta_{i,2m}\alpha_{2m, j}+\beta_{i,2m+1}\alpha_{2m+1,j}} \right){\color{blue}{+\beta_{i,2 k+1}\alpha_{2 k+1,j}}}=$
       $=\sum\limits_{m=0}^{k-1}\left({2 \over n} \cos \left({{(2l_m +1)i}\over n} \pi \right) \cos \left({{(2m+1)j}\over d} \pi \right)+{2 \over n} \sin \left({{(2l_m+1)i}\over n} \pi \right) \sin \left({{(2m+1)j}\over d} \pi \right) \right){\color{blue}{+{(-1)^{i+j} \over n}}}$ $={2 \over n}\sum\limits_{m=0}^{k-1}\cos \left({{d(2l_m+1)i-n(2m+1)j}\over {nd}} \pi \right){\color{blue}{+{(-1)^{i+j} \over n}}}$

16. Length of molecular units

    $\left| \hat \gamma_p \right| \overset{!}{=} \sqrt {d \over n}$:
    $\left| \hat \gamma_p \right| = \sqrt{\hat \gamma_p \circ \hat \gamma_p}=\sqrt{\sum\limits_{m=0}^{k-1}\alpha_{m,p}^2 \hat \beta_m \circ \hat \beta_m}=$

    1. $d=2k$ (only complex atoms involved):

       $\overset {(7.)}{=} \sqrt{{2 \over n} \sum\limits_{m=0}^{d-1}{\alpha_{m,p}^2}}$ $=\sqrt {{2 \over n} \sum\limits_{m=0}^{k-1}{\alpha_{2 m,p}^2 + \alpha_{2 m+1,p}^2}}$ $=\sqrt {{2 \over n} \sum\limits_{m=0}^{k-1}{\cos^2 \left({{(2 m+1)p} \over d} \pi \right)+ \sin^2 \left({{(2m+1)p} \over d} \pi \right)}}$ $=\sqrt{{2k}\over n}$ $=\sqrt{d \over n}$

    2. $d=2k \color{blue}+1$ (real atom involved):

       $\overset {(7.)}{=} \sqrt{\left( {2 \over n}\sum\limits_{m=0}^{k-1} \alpha_{2m,p}^2 + \alpha_{2m+1,p}^2 \right){\color{blue}{+{1 \over n} \alpha_{k,p}^2}}}$ $=\sqrt{\left({2 \over n}\sum\limits_{m=0}^{k-1}\cos^2 \left({{(2m+1)p} \over d} \pi \right)+\sin^2 \left({{(2m+1)p} \over d} \pi \right)\right){\color{blue}{+{1 \over n}\cos^2(p \pi)}}}=$
       $=\sqrt{2k{\color{blue}{+1}}\over n}$ $=\sqrt{d \over n}$

17. Orthogonality of molecular units

    $\hat \gamma_p \circ \hat \gamma_q \overset{!}{=} 0 {\color{black}{aaaa}}\forall p \ne q$:

    1. $d=2k$ (only complex atoms involved):

       $\hat \gamma_p \circ \hat \gamma_q$ $=\sum\limits_{m=0}^{d-1}\alpha_{m,p} \hat \beta_m \circ \sum\limits_{m=0}^{d-1}\alpha_{m,q} \hat \beta_m \overset{(8.)}{=} \sum\limits_{m=0}^{d-1}\alpha_{m,p} \alpha_{m,q} \hat \beta_m \circ \hat \beta_m \overset{(7.)}{=}$ ${2 \over n} \sum\limits_{m=0}^{d-1}\alpha_{m,p} \alpha_{m,q}=$
       $={2 \over n} \sum\limits_{m=0}^{k-1}\alpha_{2m,p} \alpha_{2m,q} + \alpha_{2m+1,p} \alpha_{2m+1,q}=$ $={2 \over n} \left( \sum\limits_{m=0}^{d-1}\cos \left({{(2m+1)p} \over d} \pi \right)\cos \left({{(2m+1)q} \over d} \pi \right)+\sin \left({{(2m+1)p} \over d} \pi \right)\sin \left({{(2m+1)q} \over d} \pi \right) \right)=$
       $={2 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(2m+1)(p-q)} \over d} \pi \right)$ $={1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(2m+1)(p-q)} \over d} \pi \right)+{1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(-2 m-1)(p-q)} \over d} \pi \right)=$
       $={1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(2m+1)(p-q)} \over d} \pi \right)+{1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(4 k-2 m-1)(p-q)} \over d} \pi \right)=$
       $={1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(2m+1)(p-q)} \over d} \pi \right)+{1 \over n} \sum\limits_{m=k}^{2 k-1} \cos \left({{(2 m+1)(p-q)} \over d} \pi \right)$ $={1 \over n} \sum\limits_{m=0}^{d-1} \cos \left({{(2m+1)(p-q)} \over d} \pi \right) \overset{(6.)}{=}0$

    2. $d=2k \color{blue}+1$ (real atom involved):

       $\hat \gamma_p \circ \hat \gamma_q$ $=\sum\limits_{m=0}^{d-1} \alpha_{m,p} \hat \beta_m \circ \sum\limits_{m=0}^{d-1} \alpha_{m,q} \hat \beta_m$ $\overset{(8.)}{=} \sum\limits_{m=0}^{d-1} \alpha_{m,p} \alpha_{m,q} \hat \beta_m \circ \hat \beta_m$ $\overset{(7.)}{=} \sum\limits_{m=0}^{d-1}{d_m \over n} \alpha_{m,p} \alpha_{m,q}$ $={2 \over n} \left( \sum\limits_{m=0}^{k-1} \alpha_{2m,p} \alpha_{2m,q}+\alpha_{2m+1,p} \alpha_{2m+1,q} \right)+{\color{blue}{1 \over n} \alpha_{2k,p} \alpha_{2k,q}}=$ $={2 \over n} \left( \sum\limits_{m=0}^{d-1} \cos \left({{(2m+1)p} \over d} \pi \right)\cos \left({{(2m+1)q} \over d} \pi \right)+\sin \left({{(2m+1)p} \over d} \pi \right)\sin \left({{(2m+1)q} \over d} \pi \right) \right){\color{blue}+{1 \over n}\cos \left({{(2k+1)p} \over d} \pi \right)\cos \left({{(2k+1)q} \over d} \pi \right)}=$ $={2 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(2m+1)(p-q)} \over d} \pi \right){\color{blue}+{1 \over n}\cos(p \pi)\cos(q \pi)}=$
       $={1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(2m+1)(p-q)} \over d} \pi \right)+ {1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(-2m-1)(p-q)} \over d} \pi \right){\color{blue}+{1 \over n}\cos((p-q) \pi)}=$
       $={1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(2m+1)(p-q)} \over d} \pi \right)+ {1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(4k+2-2m-1)(p-q)} \over d} \pi \right){\color{blue}+{1 \over n}\cos ((p-q) \pi)}=$
       $={1 \over n} \sum\limits_{m=0}^{k-1} \cos \left({{(2m+1)(p-q)} \over d} \pi \right)+ {1 \over n} \sum\limits_{m=k+1}^{2 k} \cos \left({{(2m+1)(p-q)} \over d} \pi \right){\color{blue}+{1 \over n}\cos \left({{(2k+1)(p-q)} \over d} \pi \right)}=$
       $={1 \over n} \sum\limits_{m=0}^{d-1} \cos \left({{(2 m+1)(p-q)} \over d} \pi \right)$ $ \overset{(6.)}{=}0$