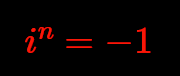
It is strange, but from the mathematical perspective this product is not really new.
It is classified as polynomial quotient ring $\mathbb R[X]/(X^n+1)$.
$\mathbb C^k$-vectors are also not new.
To define the product as complex operations in each line, was also allowed.

So what is new in this vector multiplication?
And has it any further relevance for our live?

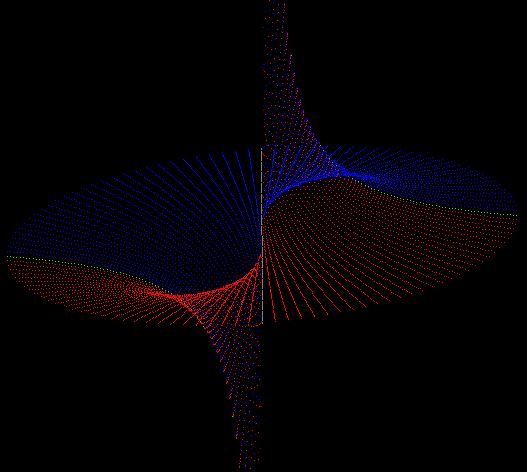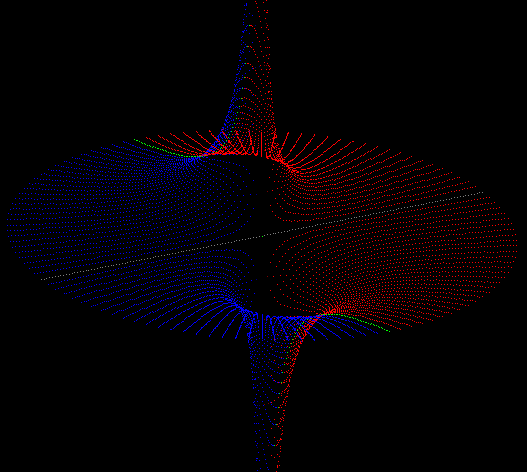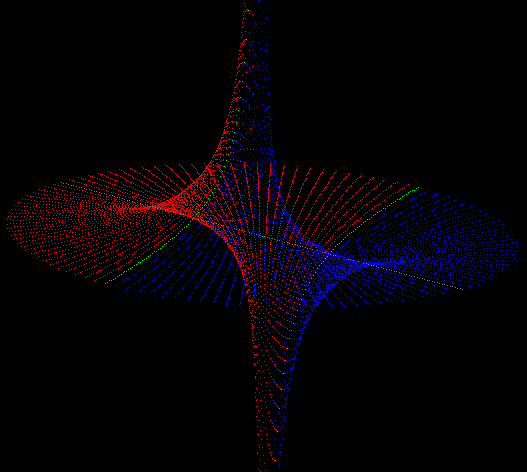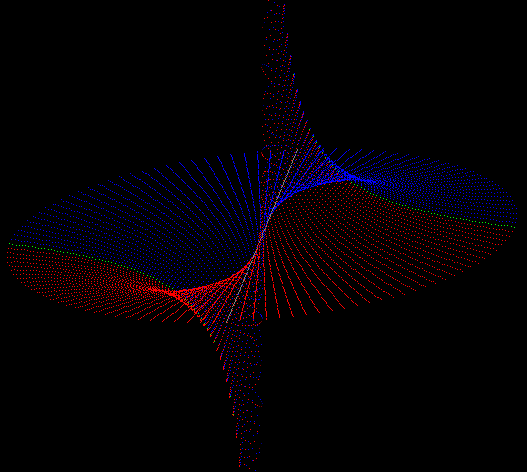
This vector multiplication is general enough to be a partner on 'same level' for vector addition.
So the full complex - and real analysis could be generalized.

It opens a new perspective toward the understanding of multi-dimensionality.
The unfolding of the reference point into vector subspaces of zero divisors is a natural concesquence of this vector multiplication.
And all this reference spaces show just a d-dimensional aspect of the full picture.
So all understanding can be always extended by further complex atoms.

For what it can be used, i have only one really useful and practical topic from physics:

If the electric charge is the real dimension of a 6-dimensional reference space:

• Then there are 3 atoms and 3 molecules within this reference space.
• Their real units will have as real coordinate $1 \over 3$ and $2 \over 3$.
• So the charge of quarks in QED (quantum electro dynamic) is easy to explain with units (and their additive inverses).
• Further their 'color charge' in QCD (quantum chromo dynamic) is easy to replace by the index of atoms and molecules.
• The 'white particle postulate' can be explained as construction of 1 in the real coordinate and annihilation in all the other 5 coordinates.

So, that's all!

I hope there are no big mistakes in the text and proofs, but i am not really a mathematician and english is also not my favorite language.
My intention was never precision, but understanding. (Still i hope, i was pretty precise, almost like a mathematician.)
In my experience the learning of facts is just knowledge, but understanding is much more!

And for that everybody must use the own brain, wire the own synapsis, etc...