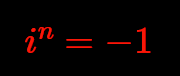
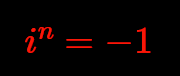
To extend the list of not perfect vector multiplications, here is the multiplication matrix $M_{\vec x}$ for the new one:

$\forall \vec x, \vec y \in \mathbb R^n$: $\vec x \cdot \vec y = {\begin{pmatrix}{x_0} & {-x_{n-1}} & {-x_{n-2}} & {\cdots} & {-x_1} \\ {x_1} & {x_0} & {-x_{n-1}} & {\cdots} & {-x_2} \\ {x_2} & {x_1} & {x_0} & {\cdots} & {-x_3} \\ {\vdots} & {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {x_{n-1}} & {x_{n-2}} & {x_{n-3}} & {\cdots} & {x_0} \end{pmatrix}} \cdot \vec y$

This matrix is the generalization of the multiplication matrix of the complex product.

Single coordinates of the product can be expressed as: $(\vec x \cdot \vec y)_k = \sum\limits_{j=0}^k x_{k-j}y_j - \sum\limits_{j=k+1}^{n-1} x_{n+k-j}y_j$.

To highlight unit vectors I am using in the follwing the denotation of physicist with a hat.

The multiplicative identity or neutral element of multiplication is the first unit of the vector space, its real unit:

$1 = \hat e_0=\begin{pmatrix} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{pmatrix} $

Imaginary unit of the vectorspace is its second unit:

$i = \hat e_1=\begin{pmatrix} 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}$

The power row of the imaginary unit goes cyclically through all units of the vector space and their additive inverses: $\forall 0 \le k < n: \space \space \space \hat e_k=i^k=-i^{k+n}$. Specially it is: $i^n=-1$.

The multiplication is associative, commutative and over the vector addition distributive.

The multiplication with a scalar $x$ is equivalent to the multiplication with $x \hat e_0$.

The set of $\mathbb R^n$-vectors with vector addition and this multiplication is isomorphicto the polynomial quotient ring $\mathbb R[X]/(X^n+1)$.
For $n=1$ and $n=2$ they are the fields $\mathbb R$ and $\mathbb C$.
For $n>2$ they are only associative, commutative rings, because of the existence of nonzero zero divisors, vectors without multiplicative inverse vectors, which we have to check properly on the next page...