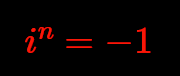
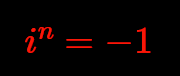
Euler's identity contains all the really important constants and operations of mathematics:

$0=1+e^{iπ}$

• the neutral element of addition, the reference $0$
• the neutral element of multiplication, the unit $1$
• the natural base of power and logarithm $e$
• the imaginary unit $i$
• and the circle constant $π$

Within these five is the imaginary unit i the only non real number. Based on this number (and equations like Euler's identity) mathematics found in the complex numbers the most effective system for calculations. Within the 2-dimensional space of the complex numbers we can calculate almost everything, only two operations are forbidden:

• the division by zero
• and the logarithm of zero

But the classical way to define the imaginary unit with $i^2=-1$, contains the constant 2, which wasn't important enough to appear in Euler's equation. That reason is good enough to replace it by something more important, the natural variable n:

$i^n=-1$

Now this equation defines i, the first non real unit of an n-dimensional space of numbers. With this explanation we indirectly excluded the cases n=0 and n=1, where a first non real unit makes no sense.

For a mathematician this equation should look more pleasant, more aesthetic, mainly more general than the original one.
And it is...