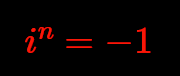
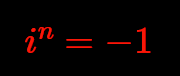
For the complex numbers $\mathbb{C}$ there are many different ways of defintion and representations. In Hamilton's approach they are the set $\mathbb{R}^2$ of ordered pairs of real numbers, or briefly $\mathbb{R}^2$-vectors.

Vectors are elements of vector spaces, which are defined over fields, for example $\mathbb Q$, $\mathbb R$ or $\mathbb C$. Fields are sets with two binary operations, addition (+) and multiplication ($\cdot$), which together satisfy the field axioms for arbitrary members $a$, $b$ and $c$ of the set:

• associativity for both operations: $a+(b+c)=(a+b)+c$, and $a \cdot (b \cdot c)=(a \cdot b) \cdot c$.
• commutativity for both operations: $a+b=b+a$, and $a \cdot b=b \cdot a$.
• additive identity (additive neutral element 0): $a+0=a$.
• multiplicative identity (multiplicative neutral element 1): $a \cdot 1=a$.
• additive inverse $-a$ exists for every element $a$: $a-a=0$.
• multiplicative inverse $a^{-1}$ exists for every element $a \ne 0$: $a \cdot a^{-1}=1$.
• distributivity of multiplication over addition: $a \cdot (b+c)=(a \cdot b)+(a \cdot c)$.

To be a field, the set and the operations must behave 'normal' like we know from the real numbers.

In the vectorial representation of the complex numbers, where $z=a+ib$ is written $\vec{z}={\small \begin{pmatrix} {a} \\ {b} \end{pmatrix}}$ or even more vectorial with indexed coordinates as $\vec{z}={\small \begin{pmatrix}{z_0}\\{z_1} \end{pmatrix}}$, the multiplication is defined with the matrix representation of the first factor: $\vec{z}\cdot \vec{w} = {\small \begin{pmatrix}{z_0} & {-z_1} \\ {z_1} & {z_0} \end{pmatrix}} \cdot \vec{w} $.

The indexing of the coordinates I started by zero, in the way like programmers do and in the same way, like i mirrored Euler's equation in the preamble, just to start with the ultimate reference point, zero.

For $\mathbb R^{n>2}$-vectors there is no 'normal' multiplication available, which could satisfy all field axioms.

• the multiplication with a scalar, where one factor is not a vector
• the scalar product of $\mathbb R^n$-vectors results in a scalar, not in a vector
• the cross product for $\mathbb R^3$-vectors is anticommutative, nonassociative and missing multiplicative inverse vectors
• the Hamilton product for the quaternions $\mathbb H = \mathbb R^4$ is noncommutative
• the product for octonions $\mathbb O = \mathbb R^8$ is nonassociative

Further it is prooven, beyond the already mentioned ones ($\mathbb R$, $\mathbb C$, $\mathbb H$ and $\mathbb O$) there are no more division algebras over the real numbers. And this hurts badly:

If there are zero divisors, elements without multiplicative inverse, we have to give up the very useful rule: a product is only then zero, if at least one of its factors is zero.

And still, the generalization of the complex numbers, by replacing 2 with n is worth of further investigations.
I can promise some surpising results...